√Contoh Bilangan Komposit – Pengertian, Cara Hitung, Himpunan

Contoh Bilangan Komposit – Pengertian, Cara Hitung, Himpunan - Jangan lupa bahagia!! yup kami juga bahagia karena Anda sudah mengunjungi situs Quipper yang saat ini sedang Anda baca. Pada kesempatan yang asik ini kita akan mengulas mengenai Contoh Bilangan Komposit – Pengertian, Cara Hitung, Himpunan secara lengkap dengan harapan bisa menjawab rasa penasaran Anda.

Namanya juga mencari informasi, tentu dibutuhkan keterbukaan dari Anda, dalam artian bahwa apa yang akan kami jelaskan disini tentu membutuhkan sedikit waktu dalam membacanya baru bisa memahaminya. Untuk itu buka lebar-lebar pikiran Anda supaya dapat menangkap "pengetahuan" baru yang akan kami bahas sebentar lagi. Berikut penjelasannya.

Pembahasan Lengkap Contoh Bilangan Komposit – Pengertian, Cara Hitung, Himpunan

Contoh Bilangan Komposit – Hay sahabat semua.! Pada perjumpaan kali ini kembali akan quipper.co.id sampaikan pembahasan materi makalah tentang contoh bilangan komposit.

Namun pada perjumpaan sebelumnya, yang mana kami juga telah menyampaikan materi makalah tentang Deret Geometri. Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini maka, mari simak ulasan selengkapnya di bawah ini.

Pengertian Bilangan Komposit

Apa yang dimaksud dengan bilangan komposit? Bilangan komposit adalah merupakan bilangan yang asli lebih dari angka satu dan bukan termasuk dalam bilangan prima.

Bilangan komposit di nyatakan sebagai faktorisasi dalam bilangan bulat, atau pun jumlah dari perkalian dari dua bilangan prima atau bilangan lebih.

Ada 10 bilangan komposit Yang pertama yaitu 6 ,8, 9, 10, 12, 15, dan 18. Bisa juga dapat disebut sebagai huruf yang memiliki faktor angka lebih dari angka dua.

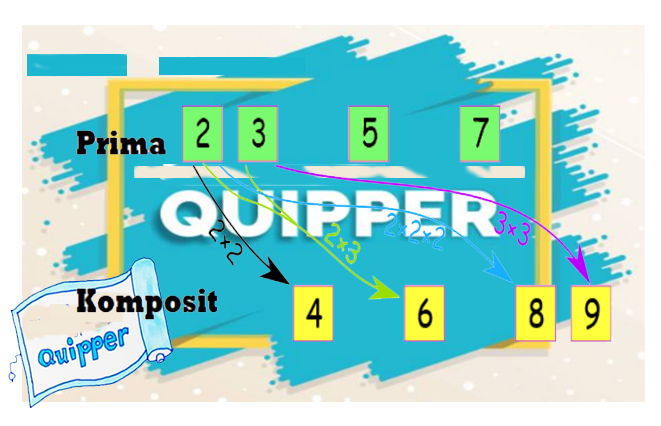
Lambang Himpunan Bilangan Komposit

Lambang bilangan komposit adalah huruf ”K” besar.

Himpunan Bilangan Komposit

Himpunan Dalam Suatu Bilangan Kompositnya Yang Kurang Dari 10
K=4,6,8,dan 9.
Yang memilik arti dari anggota himpunan dalam bilangan komposit tersebut yang berkurang dari sepuluh yaitu yang berjumlah 4.

Himpunan Bilangan Komposit Berawal
K=4,6,8,9,10,12,14,15,16 dan 18.

Himpunan Bilangan Kompositnya Yang Kurang Dari Dua Puluh
K=4,6,8,9,10,12,14,15,16 dan 18.
Yang mempunyai arti himpunan bilangan pada bilangan komposit yang artinya kurang dari 20 memiliki arti berjumlah 10.

Contoh Bilangan Komposit

Bilangan komposit kurang dari Angka 10
Ialah :4,6,8 dan 9.

10 Bilangan komposit pertama
Ialah :4,6,8,9,10,12,14,15,16 dan 18.

Bilangan komposit kurang dari angka 20
Ialah :4,6,8,9,10,12,14,15,16 dan 18.

Bilangan komposit dari pelemparan sebuah dadu
Ialah : 4 sama 6.

Bilangan kompositnya yang kurang dari 15
Ialah : 4, 6, 8,9,10,12 dan 14.

Bilangan komposit yang kurang dari 11
Ialah :4,6,8, 9 dan 10.

Bilangan komposit 1 sampai 50
Ialah :4,6,8,9,10,12,14,15,16,18,20,21,22,24,25,26,27,28,30,32,33,34,35,36,38,39,40,42,44,45,46,48 dan 49.

Cara Mengetahui Bilangan Komposit

Angka 4 termasuk bilangan komposit :

Angka 4 dapat di bagi dengan angka 1,2, dan 4.
Di bagi pada angka 1 (4:1=4)
Di bagi sama diri sendiri (4:4=1)
Di bagi pada bilangan lain (4:2=2) syarat Komposit
Hingga dapat bisa di ketahui bahwa angka4 mudah di dapatkan dari perkalian 2 bilangan prima ialah 2 × 2.

Angka 7 bukan bilangan komposit dan mengapa begitu ? Karena pada angka 7 cuma bisa di bagi dengan angka 1 dan 7, sehingga angka 7 hanya memiliki 2 faktor. Angka 7 adalah bilangan prima.

Bilangan komposit ialah merupakan bila’ngan asli yang lebih besar yang bukan bilangan prima dan dapat disebut sebagai bilangan yang memiliki faktor berjumlah lebih dari dua.

Bilangan itu dapat juga disebut sebagai faktorisasi pada bilangan yang bulat dan mempunyai hasil dari perkalian dua bilangan prima atau lebih.

Contohnya :
2×2(x2)= 8 atau 2×2=4 atau 2^3= 8 dan 2^2=4
3x3x3=27 atau 3×3=9 atau 3^3=27 dan 3^2=9
Jadi kesimpulan nya adalah apabila ada perkalian 2 pada bilangan prima atau pun lebih maka bilangan tersebut adalah dimaksud dengan bilangan komposit.

Selain dengan bilangan komposit, ada juga bilangan cacah ialah himpunan bilangan yang terdiri atas bilangan bulat dari angka 0 dan bukan bilangan negatif.

Contoh bilangan cacah :0,1,2,3,4,5,6,7,8,9,10,11,12,13,… dan seterusnya.

Sedangkan bilangan cacah dibentuk dari bilangan asli dan menambahkan nol di depannya. Bilangan cacah memiliki simbol “C” dan penulisannya ialah :

C= {0, 1, 2, 3,4, 5, 6, 7, 8, 9, 10, 11, 12, 13,…}

Operasi Bilangan Cacah :

Operasi Penjumlahan pada Bilangan Cacah

Ialah :
Sifat indentitas. (Contoh: a + 0 = 0 + a ).
Sifat pengelompokan. (Contoh ( a + b ) + c = a ( b + c ).
Sifat pertukaran. Contoh ( a + b = b + a).

Operasi Pengurangan Bilangan Cacah

Kebalikan dari operasi penjumlahan
Contoh a + b = c disebut dengan b + c = a ( a lebih besar dari b ).
a – b = b – a (bila kedua bilangan mempunyai nilai yang sama, a = b ).

Operasi Perkalian Pada Bilangan Cacah

Kali – kalian pada bilangan cacah adalah hasil yang memiliki penjumlahan yang berulang-ulang dari bilangan cacah yang sudah dikalikan.
Misalnya : 2×4=4+4 apabila 4 x 2 = 2 + 2 + 2 + 2.

Operasi Pembagian Bilangan Cacah

Operasi pembagian dalam bilangan cacah yang memiliki sifat berulang.
Contoh: 10:2=10-2-2-2-2-2
Jumlah dari pembagian diatas ialah jumlah dari pengulangan angka yang habis di kurangkan, pada contoh tersebut hasilnya adalah 5.

Dalam operasi pada pembagian bilangan cacah diatas memiliki sifat pengelompokan, distributif, pertukaran, dan identitas tak berlaku.

Nah demikianlah pembahasan materi makalah kali ini tentang contoh bilangan komposit. semoga bermanfaat dan dapat membantu teman-teman semua.

Quipper.co.id